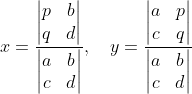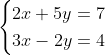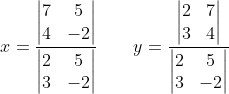中学２年生で連立方程式を習いますが
解法といえば加減法か代入法のいずれかですよね

グラフを書いて求めるという方法も
ないわけではありませんが……

きょうはそれ以外の方法
クラメルの公式を使って
連立方程式を解いてみましょう

まずはこちらを見てください

これは行列式といって
大学の数学で出てくるものです
（小生の頃は高校範囲でした）

計算はこのようになります

ではいよいよ連立方程式の登場です

これをクラメルの公式では次のように解きます

どうしてこうなるのかは説明しません
スマホの仕組みはわからないのに
スマホを使うようなものです

分子のpとqの位置だけ気をつければ
覚えるのはそう難しくありません

ただしad – bc =０になる場合は
分母が０になってしまうため
この公式は使えません

では実際に解いてみましょう

これを加減法で解く場合
係数を最小公倍数でそろえ
分数を扱わなければならず
少々手間がかかりますね

そこでクラメルの公式を使って解いてみましょう

a = 2, b = 5, c = 3, d = -2, p = 7, q = 4ですから
次のようになります
（LaTeX難しい！）

 

 

 

 

 

いかがでしたか
検算にもおすすめですよ

次回は「連立方程式を算木で解こう！」でしょうか